Question 1
A five-digit number has four equal digits and the sum of the digits is 43. Which one is the different digit?
(A) 1 (B) 3 (C) 5 (D) 7 (E) 9
Question 2
Balloons are sold in packs of 5, 10 and 25. Marius buys exactly 70 balloons. What is the smallest number of packs he could buy?
(A) 3 (B) 4 (C) 5 (D) 6 (E) 7
Question 3
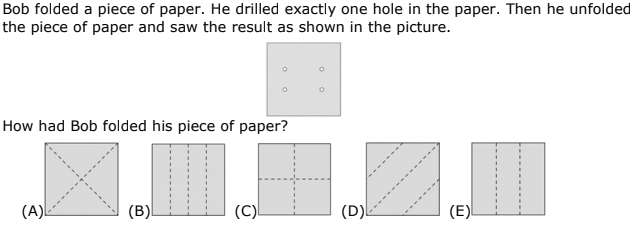
Question 4
There is a tournament at the pool. First 13 children signed up and then another 19 signed up. Six teams with an equal number of players are needed for the tournament.
At least how many more children need to sign up so that the six teams can be formed?
(A) 1 (B) 2 (C) 3 (D) 4 (E) 5
Question 5
The Modern Sofa Furniture store is selling a sofa and a loveseat made from identical modular pieces as shown in the picture.
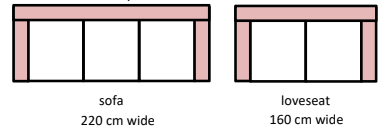
The width, including the seating and the armrests, is given below each item. How wide is an armrest?
(A) 15 cm (B) 20 cm (C) 30 cm (D) 40 cm (E) 60 cm
Question 6
David wants to cook 5 dishes on a stove with only 2 burners. The times needed to cook the 5 dishes are 40 min, 15 min, 35 min, 10 min and 45 min. What is the shortest time in which he can do it? (Once he starts cooking a dish, he may remove it from the stove only when it is cooked.)
(A) 60 min (B) 70 min (C) 75 min (D) 80 min (E) 85 min
Question 7
A mathematical test consists of 20 problems. At the beginning, everybody starts with 20 points. For a correct answer one gets 1 point, while for an incorrect or missing answer 1 point is subtracted. Mary?s final result is 24 points. How many correct answers did Mary have?
(A) 4 (B) 8 (C) 10 (D) 12 (E) 16
Question 8
Identical cubes are glued together. The figures below show the structure seen from the front, from the left, and from above.
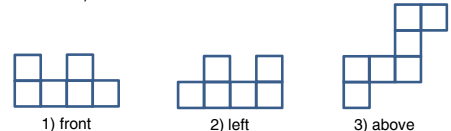
What number of cubes does the structure contain?
(A) 6 (B) 9 (C) 10 (D) 11 (E) 12
Question 9
Ten bags each contain a different number of candies from one to ten. Five boys each took two bags of candies. Alex got five candies, Bob got seven candies, Charles got nine, and Dennis got fifteen. How many candies did Eric get?
(A) 9 (B) 11 (C) 13 (D) 17 (E) 19
Question 10
George starts training at five in the afternoon. The walk from his house to the bus stop takes 5 minutes. The bus journey takes 15 minutes. It takes George 5 minutes to walk from the bus stop to the field. The bus arrives to his stop every 10 minutes from six in the morning. At what time at the latest does George have to leave his house to arrive at the field exactly on time?

Question 11
A small zoo has a giraffe, an elephant, a lion and a turtle. Susan wants to plan a tour where she sees exactly two different animals. She does not want to start with the lion.
How many different tours can she plan?
(A) 3 (B) 7 (C) 8 (D) 9 (E) 12
Question 12
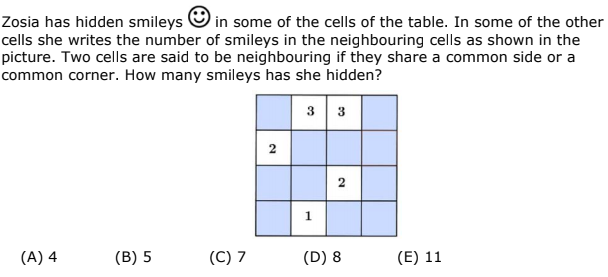
Question 13


Question 14
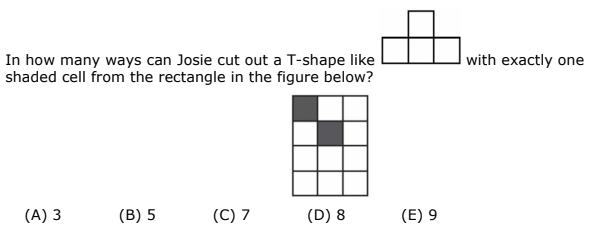
Question 15
Numbers are placed in the cells of the 4 ? 4 square shown in the picture. Mary finds the 2 ? 2 square where the sum of the numbers in the four cells is the largest. What is that sum?
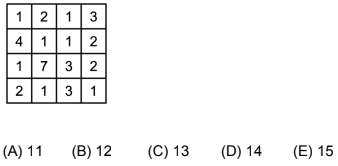
Question 16
David wants to cook 5 dishes on a stove with only 2 burners. The times needed to cook the 5 dishes are 40 min, 15 min, 35 min, 10 min and 45 min . What is the shortest time in which he can do it? (He may only remove a dish from the stove when it is cooked.)
(A) 60 min (B) 70 min (C) 75 min (D) 80 min (E) 85 min
Question 17
Which number should be written in the circle containing the question mark?
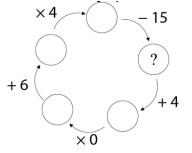
(A) 9 (B) 10 (C) 11 (D) 12 (E) 13
Question 18
The picture shows a group of building blocks and a plan of the same group. Some ink has dripped onto the plan. What is the sum of the numbers under the ink blots?
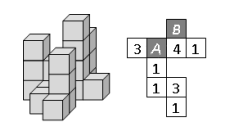
(A) 3 (B) 4 (C) 5 (D) 6 (E) 7
Question 19
How long is the train?
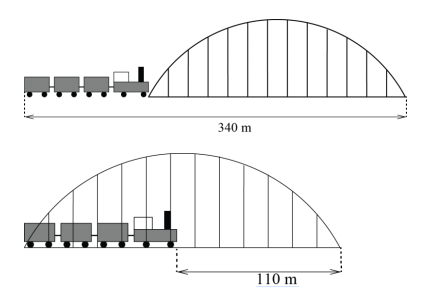
(A) 55 m (B) 115 m (C) 170 m (D) 220 m (E) 230 m
Question 20
A small zoo has a giraffe, an elephant, a lion and a turtle. Susan wants to plan a tour where she sees 2 different animals. She does not want to start with the lion. How many different tours can she plan?
(A) 3 (B) 7 (C) 8 (D) 9 (E) 12
Question 21
Four brothers have eaten 11 cookies in total. Each of them has eaten at least one cookie and no two of them have eaten the same number of cookies. Three of them have eaten 9 cookies in total and one of them has eaten exactly 3 cookies. How many cookies have been eaten by the boy who has eaten the largest number of cookies?
(A) 3 (B) 4 (C) 5 (D) 6 (E) 7
Question 22
Ten bags each contain a different number of candies from 1 to 10. Five boys each took two bags of candies. Alex got 5 candies. Bob got 7 candies, Charles got 9, and Dennis got 15. Eric took the last two bags. How many candies did Eric get?
(A) 9 (B) 11 (C) 13 (D) 17 (E) 19
Question 23
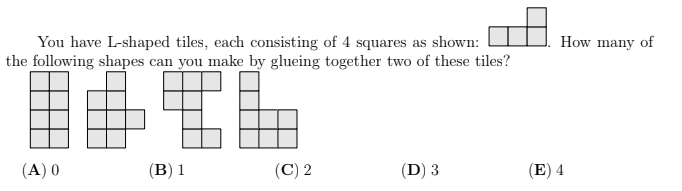
Question 24
Three balloons cost 12 cents more than one balloon. How much does one balloon cost?
(A) 4 (B) 6 (C) 8 (D) 10 (E) 12
Question 25
Grandmother made 20 gingerbread biscuits for her grandchildren. She decorated them with raisins and nuts. First she decorated 15 cakes with raisins and then 15 cakes with nuts. At least how many cakes were decorated both with raisins and nuts?
(A) 4 (B) 5 (C) 6 (D) 8 (E) 10
Question 26
In a sudoku the numbers 1, 2, 3, 4 can occur only once in each column and in each row. In the mathematical sudoku below Patrick first writes in the results of the calculations. Then he completes the sudoku. Which number will Patrick put in the grey cell?
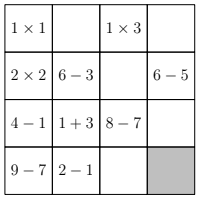
(A) 1 (B) 2 (C) 3 (D) 4 (E) 1 or 2
Question 27
Among Nikolay?s classmates there are twice as many girls as boys. Which of the following numbers can be equal to the number of all children in this class?
(A) 30 (B) 20 (C) 24 (D) 25 (E) 29
Question 28
In the animal?s school, 3 kittens, 4 ducklings, 2 goslings and several lambs are taking lessons. The teacher owl found out that all of her pupils have 44 legs altogether. How many lambs are among them?
(A) 6 (B) 5 (C) 4 (D) 3 (E) 2
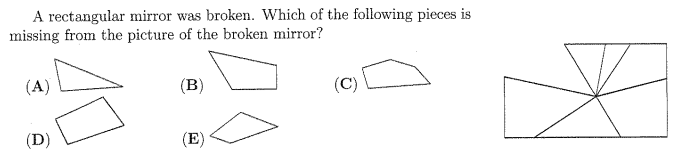
Question 29
A cuboid is made of four pieces, as shown. Each piece consists of four cubes and is a single colour. What is the shape of the white piece?
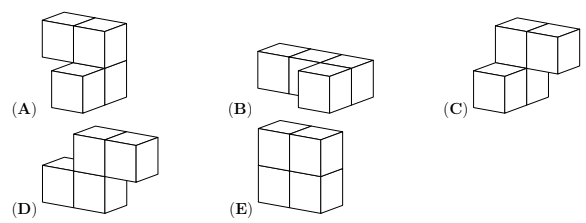
Question 30
At a Christmas party there was exactly one candlestick on each of the 15 tables. There were 6 five-branched candlesticks, the rest of them were three-branched ones. How many candles had to be bought for all the candlesticks?
(A) 45 (B) 50 (C) 57 (D) 60 (E) 75
Question 31
A grasshopper wants to climb a staircase with many steps. She makes only two different jumps: 3 steps up or 4 steps down. Beginning at the ground level, at least how many jumps will she have to make in order to take a rest on the 22th step?
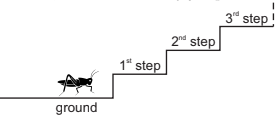
(A) 7 (B) 9 (C) 10 (D) 12 (E) 15
Question 32
Frank made a domino snake of seven tiles. He put the tiles next to each other so that the sides with the same number of dots were touching. Originally the snake had 33 dots on its back. However, his brother George took away two tiles from the snake (see the picture). How many dots were in the place with the question mark?
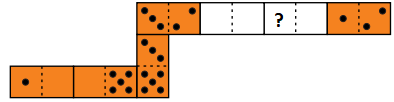
(A) 2 (B) 3 (C) 4 (D) 5 (E) 6
Question 33
Gregor forms two numbers with the digits 1, 2, 3, 4, 5 and 6. Both numbers have three digits, each digit is used only once. He adds these two numbers. What is the greatest sum Gregor can get?
(A) 975 (B) 999 (C) 1083 (D) 1173 (E) 1221
Question 34
Laura, Iggy, Val and Kate want to be in one photo together. Kate and Laura are best friends and they want to stand next to each other. Iggy wants to stand next to Laura because he likes her. In how many possible ways can they arrange for the photo?
(A) 3 (B) 4 (C) 5 (D) 6 (E) 7
Question 35
A special clock has 3 hands of different length (for hours, for minutes, and for seconds). We do not know which hand is which, but we know that the clock runs correctly. At 12:55:30 p.m. the hands were in position depicted on the right. How will this clock look like at 8:11:00 p.m.?
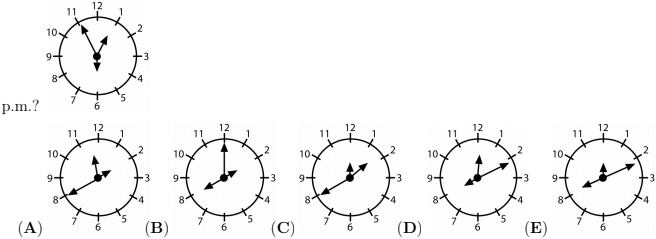
Question 36
Michael chose some positive number, multiplied it by itself, added 1, multiplied the result by 10, added 3, and multiplied the result by 4. His final answer was 2012. What number did Michael choose?
(A) 11 (B) 9 (C) 8 (D) 7 (E) 5
Question 37
A rectangular paper sheet measures 192 x 84 mm. You cut the sheet along just one straight line to get two parts, one of which is a square. Then you do the same with the non-square part of the sheet, and so on. What is the length of the side of the smallest square you can get with this procedure?
(A) 1 mm (B) 4 mm (C) 6 mm (D) 10 mm (E) 12 mm
Question 38
In a soccer game the winner gains 3 points, while the loser gains 0 points. If the game is a draw, then the two teams gain 1 point each. A team has played 38 games gaining 80 points.
Find the greatest possible number of games that the team lost.
(A) 12 (B) 11 (C) 10 (D) 9 (E) 8
Question 39
Question 40

Question 41
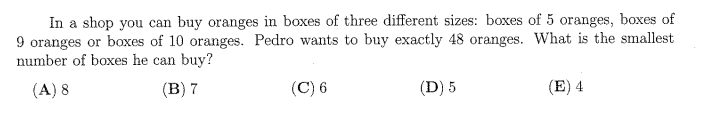
Question 42
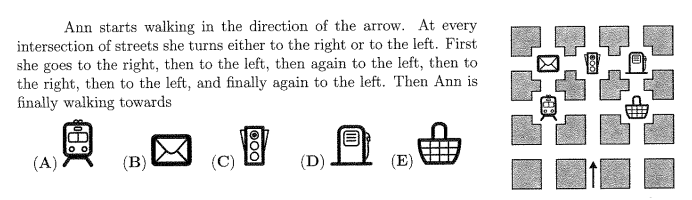
Question 43

Question 44
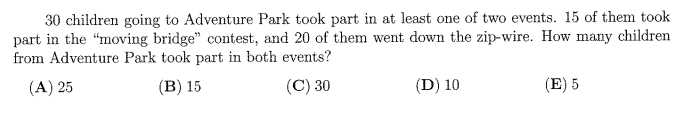
Question 45

Question 46

Question 47

Question 48

Question 49
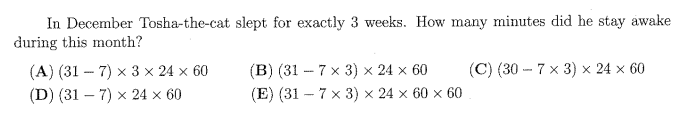
Question 50
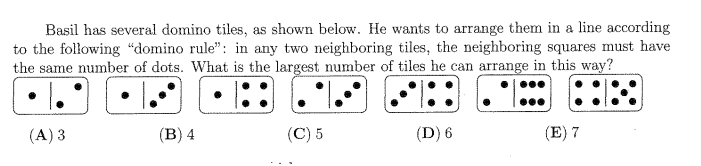
Question 51
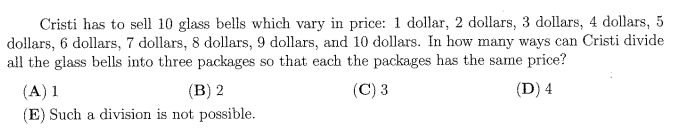
Question 52

Question 53

Question 54
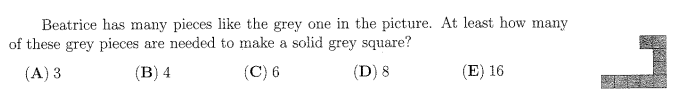
Answer Keys
Question 1: D
Question 2: B
Question 3: C
Question 4: D
Question 5: B
Question 6: C
Question 7: D
Question 8: B
Question 9: E
Question 10: A
Question 11: D
Question 12: B
Question 13: B
Question 14: D
Question 15: D
Question 16: C
Question 17: A
Question 18: C
Question 19: B
Question 20: D
Question 21: C
Question 22: E
Question 23: E
Question 24: B
Question 25: E
Question 26: C
Question 27: D
Question 28: B
Question 29: D
Question 30: C
Question 31: D
Question 32: C
Question 33: D
Question 34: B
Question 35: E
Question 36: D
Question 37: E
Question 38: C
Question 39: B
Question 40: D
Question 41: D
Question 42: A
Question 43: D
Question 44: E
Question 45: B
Question 46: B
Question 47: D
Question 48: D
Question 49: B
Question 50: C
Question 51: E
Question 52: B
Question 53: B
Question 54: B