Sample Question 23:

A regular octagon \(ABCDEFGH\) has an area of one square unit. What is the area of the rectangle \(ABEF\)?

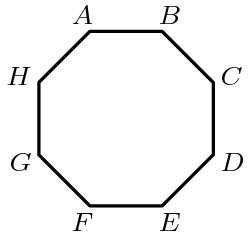\(\textbf{(A) } 1 - \frac{\sqrt{2}}{2} \qquad\textbf{(B) } \frac{\sqrt{2}}{4} \qquad\textbf{(C) } \sqrt{2} - 1 \qquad\textbf{(D) } \frac{1}{2} \qquad\textbf{(E) } \frac{1+\sqrt{2}}{4}\)

---

Answer Keys

Question 23: D

---

Solutions

Question 23
Step 1: The area of a regular octagon is given by the formula \( \frac{ap}{2}=1 \), where \( a \) is the apothem and \( p \) is the perimeter.

Step 2: This octagon's side length is \( \frac{p}{8} \) and the apothem is \( 2a \).

Step 3: The area of the rectangle \( ABEF \) is given by the formula \( \frac{p}{8} \times 2a = \frac{2ap}{8} = \frac{ap}{4} \).

Step 4: From steps 1 and 3, we can observe that the area of the rectangle is half the area of the octagon.

Step 5: Since the area of the octagon is one unit square, the area of the rectangle \( ABEF \) is \( \frac{1}{2} \) unit square.

Therefore, the answer is \(\textbf{(D)}\ \frac{1}{2}\).