To get a human or AI tutor to help you, click Register
Sample Question 14:
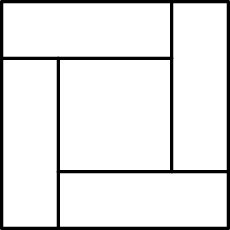
Step 1: Note that the area of the outer square is 4 times that of the inner square. Consequently, the side length of the outer square is \(\sqrt{4} = 2\) times the side length of the inner square.
Step 2: Identify the shorter side of the rectangle as \(1/4\) of the side length of the outer square and the longer side of the rectangle as \(3/4\) of the side length of the outer square.
Step 3: Calculating the ratio of the longer side to the shorter side of each rectangle, we discover that the ratio is \(3\). Thus, the answer is \(\boxed{(A)3}\).
Four congruent rectangles are placed as shown. The area of the outer square is \(4\) times that of the inner square. What is the ratio of the length of the longer side of each rectangle to the length of its shorter side?

\(\mathrm{(A)}\ 3 \qquad \mathrm{(B)}\ \sqrt {10} \qquad \mathrm{(C)}\ 2 + \sqrt2 \qquad \mathrm{(D)}\ 2\sqrt3 \qquad \mathrm{(E)}\ 4\)
Answer Keys
Question 14: ASolutions
Question 14Step 1: Note that the area of the outer square is 4 times that of the inner square. Consequently, the side length of the outer square is \(\sqrt{4} = 2\) times the side length of the inner square.
Step 2: Identify the shorter side of the rectangle as \(1/4\) of the side length of the outer square and the longer side of the rectangle as \(3/4\) of the side length of the outer square.
Step 3: Calculating the ratio of the longer side to the shorter side of each rectangle, we discover that the ratio is \(3\). Thus, the answer is \(\boxed{(A)3}\).