To get a human or AI tutor to help you, click Register
Sample Question 12:
Step 1: Note that quadrilateral \(UVCM\) has perpendicular diagonals. Therefore, the area of this quadrilateral could be found as half of the product of the length of the diagonals.
Step 2: Realize that triangle \(AUV\) has \(\frac{1}{4}\) the area of triangle \(AMC\) based on similarity rules. So, \(UVCM\) has \(\frac{3}{4}\) of the area of \(AMC\).
Step 3: Setting up the equation based on step 2, we obtain: \(\frac{1}{2} \times 12 \times 12 = \frac{3}{4} \times [AMC]\). Solving this equation gives us: \(72 = \frac{3}{4} \times [AMC]\).
Step 4: Solving this equation further, we find that the area of \(AMC\) equals to 96. The area of triangle AMC is 96 square units or \(\boxed{\textbf{(C)}\ 96}\).
Triangle \(AMC\) is isosceles with \(AM = AC\). Medians \(\overline{MV}\) and \(\overline{CU}\) are perpendicular to each other, and \(MV=CU=12\). What is the area of \(\triangle AMC?\)
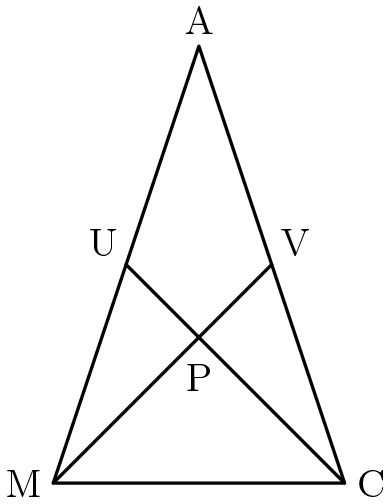
\(\textbf{(A) } 48 \qquad \textbf{(B) } 72 \qquad \textbf{(C) } 96 \qquad \textbf{(D) } 144 \qquad \textbf{(E) } 192\)
Answer Keys
Question 12: CSolutions
Question 12Step 1: Note that quadrilateral \(UVCM\) has perpendicular diagonals. Therefore, the area of this quadrilateral could be found as half of the product of the length of the diagonals.
Step 2: Realize that triangle \(AUV\) has \(\frac{1}{4}\) the area of triangle \(AMC\) based on similarity rules. So, \(UVCM\) has \(\frac{3}{4}\) of the area of \(AMC\).
Step 3: Setting up the equation based on step 2, we obtain: \(\frac{1}{2} \times 12 \times 12 = \frac{3}{4} \times [AMC]\). Solving this equation gives us: \(72 = \frac{3}{4} \times [AMC]\).
Step 4: Solving this equation further, we find that the area of \(AMC\) equals to 96. The area of triangle AMC is 96 square units or \(\boxed{\textbf{(C)}\ 96}\).