To get a human or AI tutor to help you, click Register
Sample Question 21:
Step 1: Apply Simon's Favorite Factoring Trick to rewrite the three given equations in the following form:
\((a+1)(b+1) = 525, \quad (b+1)(c+1) = 147, \quad (c+1)(d+1) = 105\)
Step 2: Define new variables \(e=a+1, f=b+1, g=c+1, h=d+1\), so we can express the above equations in terms of products of prime numbers as:
\(ef = 3 \cdot 5 \cdot 5 \cdot 7, \quad fg = 3 \cdot 7 \cdot 7, \quad gh = 3 \cdot 5 \cdot 7\)
Step 3: Notice that \(7^2\) divides \(fg\), but \(7^2\) cannot divide either \(f\) or \(g\) as it would then also divide \(ef\) or \(gh\). Therefore, \(7\) divides both \(f\) and \(g\).
Step 4: We have two possible combinations for \(f\) and \(g\): \((f,g) = (7,21)\) or \((f,g) = (21,7)\).
Step 5: For the first case \((f,g) = (7,21)\), we get \(e=75, h=5\), and therefore, the original numbers are \((a,b,c,d) = (74,6,20,4)\). However, \(a \cdot b \cdot c \cdot d\) is not equal to \(8!\) and \(a-d\) is not in the answer choices. Hence, this is not a valid solution.
Step 6: For the second case \((f,g) = (21,7)\), we get \(e=25, h=15\), and therefore the original numbers are \((a,b,c,d) = (24,20,6,14)\).
Step 7: Thus, \(a - d = 24 - 14 = 10\). Therefore, the answer to the problem is \((D)\) 10.
Four positive integers \(a\), \(b\), \(c\), and \(d\) have a product of \(8!\) and satisfy:
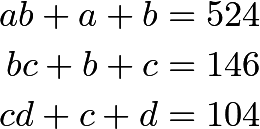
What is \(a-d\)?
\(\text{(A) }4 \qquad \text{(B) }6 \qquad \text{(C) }8 \qquad \text{(D) }10 \qquad \text{(E) }12\)
Answer Keys
Question 21: DSolutions
Question 21Step 1: Apply Simon's Favorite Factoring Trick to rewrite the three given equations in the following form:
\((a+1)(b+1) = 525, \quad (b+1)(c+1) = 147, \quad (c+1)(d+1) = 105\)
Step 2: Define new variables \(e=a+1, f=b+1, g=c+1, h=d+1\), so we can express the above equations in terms of products of prime numbers as:
\(ef = 3 \cdot 5 \cdot 5 \cdot 7, \quad fg = 3 \cdot 7 \cdot 7, \quad gh = 3 \cdot 5 \cdot 7\)
Step 3: Notice that \(7^2\) divides \(fg\), but \(7^2\) cannot divide either \(f\) or \(g\) as it would then also divide \(ef\) or \(gh\). Therefore, \(7\) divides both \(f\) and \(g\).
Step 4: We have two possible combinations for \(f\) and \(g\): \((f,g) = (7,21)\) or \((f,g) = (21,7)\).
Step 5: For the first case \((f,g) = (7,21)\), we get \(e=75, h=5\), and therefore, the original numbers are \((a,b,c,d) = (74,6,20,4)\). However, \(a \cdot b \cdot c \cdot d\) is not equal to \(8!\) and \(a-d\) is not in the answer choices. Hence, this is not a valid solution.
Step 6: For the second case \((f,g) = (21,7)\), we get \(e=25, h=15\), and therefore the original numbers are \((a,b,c,d) = (24,20,6,14)\).
Step 7: Thus, \(a - d = 24 - 14 = 10\). Therefore, the answer to the problem is \((D)\) 10.