To get a human or AI tutor to help you, click Register
Sample Question 8:
Step 1: Calculate the total sum of the faces of one die, which is \(1+2+3+4+5+6 = 21\).
Step 2: Multiply the total sum of the faces of one die by the number of dice which is \(3\), hence, \(3 * 21 = 63\).
Step 3: Count the total sum of the visible faces which is \(1, 1, 2, 3, 4, 5, 6\), thus the total is \(22\).
Step 4: Subtract the total sum of visible faces from the total of all the faces on the dice, hence, \(63 - 22 = 41\).
The total number of dots not visible is 41, so the answer is \(\text{(D) 41}\).
Three dice with faces numbered 1 through 6 are stacked as shown. Seven of the eighteen faces are visible, leaving eleven faces hidden (back, bottom, between). The total number of dots NOT visible in this view is
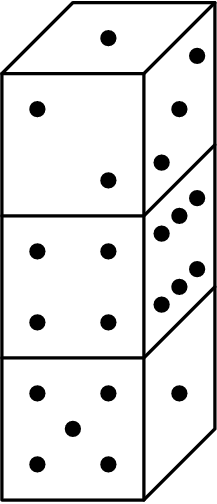
\(\text{(A)}\ 21 \qquad \text{(B)}\ 22 \qquad \text{(C)}\ 31 \qquad \text{(D)}\ 41 \qquad \text{(E)}\ 53\)
Answer Keys
Question 8: DSolutions
Question 8Step 1: Calculate the total sum of the faces of one die, which is \(1+2+3+4+5+6 = 21\).
Step 2: Multiply the total sum of the faces of one die by the number of dice which is \(3\), hence, \(3 * 21 = 63\).
Step 3: Count the total sum of the visible faces which is \(1, 1, 2, 3, 4, 5, 6\), thus the total is \(22\).
Step 4: Subtract the total sum of visible faces from the total of all the faces on the dice, hence, \(63 - 22 = 41\).
The total number of dots not visible is 41, so the answer is \(\text{(D) 41}\).