To get a human or AI tutor to help you, click Register
Sample Question 20:
Step 1: Observe that the same pattern repeats for every \(6 \times 6\) tile.
Step 2: Looking into the pattern more closely, it can be seen that there is also symmetry in the top \(3 \times 3\) square.
Step 3: From this observation, it can be concluded that the fraction of the entire floor tiled with dark tiles is the same as the fraction in the \(3 \times 3\) square.
Step 4: Count the tiles in the \(3 \times 3\) square. There are \(4\) dark tiles and \(9\) total tiles.
Step 5: The fraction of the \(3 \times 3\) square made up of dark tiles is therefore \(4/9\), which is the same fraction as that of the entire floor. Therefore, the answer is \(\text{(B)}\ \frac{4}{9}\).
A corner of a tiled floor is shown. If the entire floor is tiled in this way and each of the four corners looks like this one, then what fraction of the tiled floor is made of darker tiles?
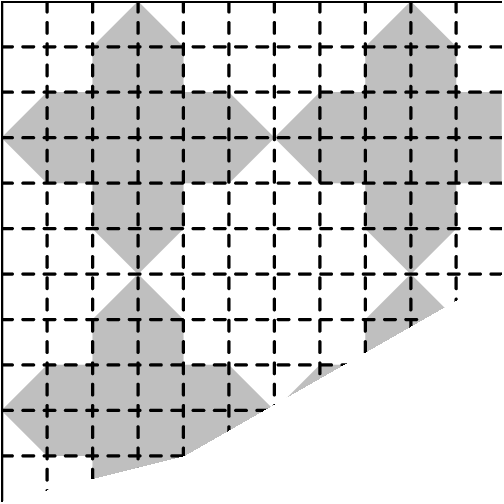
\(\text{(A)}\ \frac{1}{3} \qquad \text{(B)}\ \frac{4}{9} \qquad \text{(C)}\ \frac{1}{2} \qquad \text{(D)}\ \frac{5}{9} \qquad \text{(E)}\ \frac{5}{8}\)
Answer Keys
Question 20: BSolutions
Question 20Step 1: Observe that the same pattern repeats for every \(6 \times 6\) tile.
Step 2: Looking into the pattern more closely, it can be seen that there is also symmetry in the top \(3 \times 3\) square.
Step 3: From this observation, it can be concluded that the fraction of the entire floor tiled with dark tiles is the same as the fraction in the \(3 \times 3\) square.
Step 4: Count the tiles in the \(3 \times 3\) square. There are \(4\) dark tiles and \(9\) total tiles.
Step 5: The fraction of the \(3 \times 3\) square made up of dark tiles is therefore \(4/9\), which is the same fraction as that of the entire floor. Therefore, the answer is \(\text{(B)}\ \frac{4}{9}\).