Mechanical and Longitudinal
What is sound wave? Sound wave is a disturbance that is transported through a medium (air, water, steel, etc.) via the mechanism of particle-to-particle interaction, a sound wave is characterized as a mechanical wave.
The generation and propagation of a sound wave is demonstrated in the animation below.

When sound wave travels through air, the vibrations of the particles are best described as longitudinal. Longitudinal waves are waves in which the motion of the individual particles of the medium is in a direction that is parallel to the direction of energy transport.
How are the longitudinal sound waves produced? A vibrating string can create longitudinal waves as depicted in the animation below. As the vibrating string moves in the forward direction, it begins to push upon surrounding air molecules, moving them to the right towards their nearest neighbor. This causes the air molecules to the right of the string to be compressed into a small region of space. As the vibrating string moves in the reverse direction (leftward), it lowers the pressure of the air immediately to its right, thus causing air molecules to move back leftward. The lower pressure to the right of the string causes air molecules in that region immediately to the right of the string to expand into a large region of space. The back and forth vibration of the string causes individual air molecules (or a layer of air molecules) in the region immediately to the right of the string to continually vibrate back and forth horizontally. The molecules move rightward as the string moves rightward and then leftward as the string moves leftward. These back and forth vibrations are imparted to adjacent neighbors by particle-to-particle interaction. Other surrounding particles begin to move rightward and leftward, thus sending a wave to the right. Since air molecules (the particles of the medium) are moving in a direction that is parallel to the direction that the wave moves, the sound wave is referred to as a longitudinal wave. The result of such longitudinal vibrations is the creation of compressions and rarefactions within the air.

Because of the longitudinal motion of the air particles, there are regions in the air where the air particles are compressed together and other regions where the air particles are spread apart. These regions are known as compressions and rarefactions respectively. The compressions are regions of high air pressure while the rarefactions are regions of low air pressure.
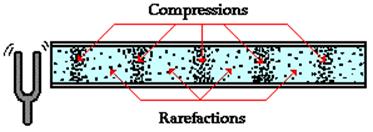
Transverse wave’s wavelength is commonly measured from one wave crest to the next adjacent wave crest or from one wave trough to the next adjacent wave trough. Since a longitudinal wave does not contain crests and troughs, its wavelength must be measured differently. A longitudinal wave consists of a repeating pattern of compressions and rarefactions. Thus, the longitudinal wave’s wavelength is commonly measured as the distance from one compression to the next adjacent compression or the distance from one rarefaction to the next adjacent rarefaction.
Since a sound wave consists of a repeating pattern of high-pressure and low-pressure regions moving through a medium, it is sometimes referred to as a pressure wave.
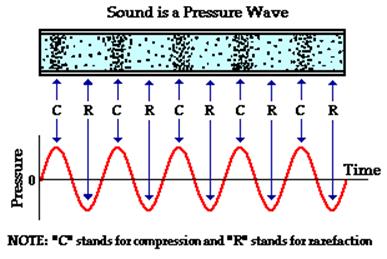
The representation of sound by a sine wave is merely an attempt to illustrate the sinusoidal nature of the pressure-time fluctuations. Do not conclude that sound is a transverse wave that has crests and troughs.
Audible Frequency Range, Pitch
The human ear is capable of detecting sound waves with a wide range of frequencies, ranging between approximately 20 Hz to 20 000 Hz. Any sound with a frequency below the audible range of hearing (i.e., less than 20 Hz) is known as an infrasound and any sound with a frequency above the audible range of hearing (i.e., more than 20 000 Hz) is known as an ultrasound. Humans are not alone in their ability to detect a wide range of frequencies. Dogs can detect frequencies as low as approximately 50 Hz and as high as 45 000 Hz. Cats can detect frequencies as low as approximately 45 Hz and as high as 85 000 Hz. Bats, being nocturnal creature, must rely on sound echolocation for navigation and hunting. Bats can detect frequencies as high as 120 000 Hz. Dolphins can detect frequencies as high as 200 000 Hz. While dogs, cats, bats, and dolphins have an unusual ability to detect ultrasound, an elephant possesses the unusual ability to detect infrasound, having an audible range from approximately 5 Hz to approximately 10 000 Hz.
The sensation of a frequency is commonly referred to as the pitch of a sound. A high pitch sound corresponds to a high frequency sound wave and a low pitch sound corresponds to a low frequency sound wave.
Sound Intensity
The amount of energy that is transported past a given area of the medium per unit of time is known as the intensity of the sound wave. The greater the amplitude of vibrations of the particles of the medium, the greater the rate at which energy is transported through it, and the more intense that the sound wave is. Intensity is the energy / (time * area); and since the energy/time ratio is equivalent to the quantity power, intensity is simply the power/area.

Typical units for expressing the intensity of a sound wave are Watts/meter2.
As a sound wave carries its energy through a two-dimensional or three-dimensional medium, the intensity of the sound wave decreases with increasing distance from the source.  The decrease in intensity with increasing distance is explained by the fact that the wave is spreading out over a circular (2 dimensions) or spherical (3 dimensions) surface and thus the energy of the sound wave is being distributed over a greater surface area.
The decrease in intensity with increasing distance is explained by the fact that the wave is spreading out over a circular (2 dimensions) or spherical (3 dimensions) surface and thus the energy of the sound wave is being distributed over a greater surface area.
The mathematical relationship between intensity and distance is sometimes referred to as an inverse square relationship.
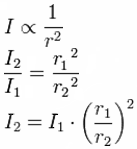
The intensity varies inversely with the square of the distance from the source.
|
Distance |
Intensity |
|
1 m |
160 units |
|
2 m |
40 units |
|
3 m |
17.8 units |
|
4 m |
10 units |
The scale for measuring intensity is the decibel scale.
The threshold of hearing is assigned a sound level of 0 decibels (abbreviated 0 dB); this sound corresponds to an intensity of 1*10-12 W/m2.
A sound that is 10 times more intense (1*10-11 W/m2) is assigned a sound level of 10 dB.
A sound that is 10*10 or 100 times more intense (1*10-10 W/m2) is assigned a sound level of 20 db.
A sound that is 10*10*10 or 1000 times more intense (1*10-9 W/m2) is assigned a sound level of 30 db.
A sound that is 10*10*10*10 or 10000 times more intense (1*10-8 W/m2) is assigned a sound level of 40 db.
While the intensity of a sound is a very objective quantity that can be measured with sensitive instrumentation, the loudness of a sound is more of a subjective response that will vary with a number of factors. The same sound will not be perceived to have the same loudness to all individuals. Age is one factor that affects the human ear's response to a sound.
Reflection, Refraction, and Dffraction
Reflection involves a change in direction of waves when they bounce off a barrier.

Refraction of waves involves a change in the direction of waves as they pass from one medium  to another. Refraction is the bending of the path of the waves.
to another. Refraction is the bending of the path of the waves.
Refraction is accompanied by a change in speed and wavelength of the waves. The speed of a wave is dependent upon the properties of the medium through which the waves travel. So if the medium (and its properties) is changed, the speed of the waves is changed.
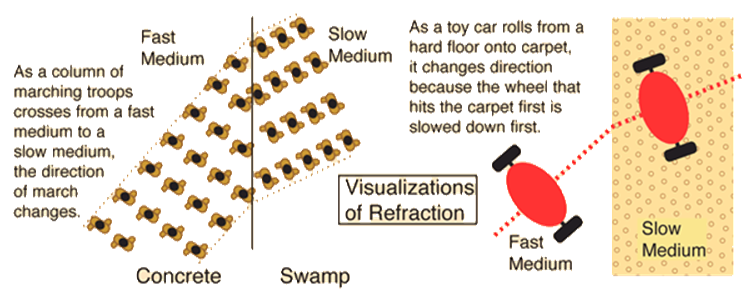
Why change in speed will result in a change in direction? A column of troops approaching a medium where their speed is slower as shown will turn toward the right because the right side of the column hits the slow medium first and is therefore slowed down. The marchers on the left, perhaps oblivious to the plight of their companions, continue to march ahead full speed until they hit the slow medium.
The most significant property of water that would affect the speed of waves traveling on its surface is the depth of the water. Water waves travel fastest when the medium is the deepest. Thus, if water waves are passing from deep water into shallow water, they will slow down. This decrease in speed will also be accompanied by a decrease in wavelength. So as water waves are transmitted from deep water into shallow water, the speed decreases, the wavelength decreases, and the direction changes.
Diffraction is the bending of waves around small (compared to the wavelength) obstacles and the spreading out of waves beyond small (compared to the wavelength) openings.

The fact that you can hear sounds around corners and around barriers involves both diffraction and reflection of sound. Diffraction in such cases helps the sound to "bend around" the obstacles.
The thunder from a close bolt of lightning will be experienced as a sharp crack, indicating the presence of a lot of high frequency sound. The thunder from a distant strike will be experienced as a low rumble since the long wavelengths can bend around obstacles to get to you. There are other factors such as the higher air absorption of high frequencies involved, but diffraction plays a part in the experience.
An implication of diffraction is the fact that a wave which is much longer than the size of an obstacle, like the post in the auditorium above, cannot give you information about that obstacle. A fundamental principle of imaging is that you cannot see an object which is smaller than the wavelength of the wave with which you view it. You cannot see a virus with a light microscope because the virus is smaller than the wavelength of visible light. The reason for that limitation can be visualized with the auditorium example: the sound waves bend in and reconstruct the wavefront past the post. When you are several sound wavelengths past the post, nothing about the wave gives you information about the post. So your experience with sound can give you insights into the limitations of all kinds of imaging processes.
Diffraction has a dual nature, since the same phenomenon which causes waves to bend around obstacles causes them to spread out past small openings. This aspect of diffraction also has many implications. Besides being able to hear the sound when you are outside the door as in the illustration above, this spreading out of sound waves has consequences when you are trying to soundproof a room. Good soundproofing requires that a room be well sealed, because any openings will allow sound from the outside to spread out in the room.
Sound Wave Interference
How can sound waves that do not possess upward and downward displacements interfere constructively and destructively? Sound is a pressure wave that consists of compressions and rarefactions. As a compression passes through a section of a medium, it tends to pull particles together into a small region of space, thus creating a high-pressure region. And as a rarefaction passes through a section of a medium, it tends to push particles apart, thus creating a low-pressure region. The interference of sound waves causes the particles of the medium to behave in a manner that reflects the net effect of the two individual waves upon the particles.
For example, if a compression (high pressure) of one wave meets up with a compression (high pressure) of a second wave at the same location in the medium, then the net effect is that that particular location will experience an even greater pressure. This is a form of constructive interference. If two rarefactions (two low-pressure disturbances) from two different sound waves meet up at the same location, then the net effect is that that particular location will experience an even lower pressure. This is also an example of constructive interference. Now if a particular location along the medium repeatedly experiences the interference of two compressions followed up by the interference of two rarefactions, then the two sound waves will continually reinforce each other and produce a very loud sound. The loudness of the sound is the result of the particles at that location of the medium undergoing oscillations from very high to very low pressures. Locations along the medium where constructive interference continually occurs are known as anti-nodes.
Now if two sound waves interfere at a given location in such a way that the compression of one wave meets up with the rarefaction of a second wave, destructive interference results. The net effect of a compression (which pushes particles together) and a rarefaction (which pulls particles apart) upon the particles in a given region of the medium is to not even cause a displacement of the particles. The tendency of the compression to push particles together is canceled by the tendency of the rarefactions to pull particles apart; the particles would remain at their rest position as though there wasn't even a disturbance passing through them. This is a form of destructive interference. Now if a particular location along the medium repeatedly experiences the interference of a compression and rarefaction followed up by the interference of a rarefaction and a compression, then the two sound waves will continually cancel each other and no sound is heard. The absence of sound is the result of the particles remaining at rest and behaving as though there were no disturbance passing through it. Amazingly, in a situation such as this, two sound waves would combine to produce no sound. Locations along the medium where destructive interference continually occurs are known as nodes.
The destructive interference of sound waves can also be used advantageously in noise reduction systems. Earphones have been produced that can be used by factory and construction workers to reduce the noise levels on their jobs. Such earphones capture sound from the environment and use computer technology to produce a second sound wave that one-half cycle out of phase. The combination of these two sound waves within the headset will result in destructive interference and thus reduce a worker's exposure to loud noise.
Musical Beats
Beats are the periodic and repeating fluctuations in the intensity of a sound when two sound waves of very similar frequencies interfere with one another. The diagram below illustrates the wave interference pattern resulting from two waves (drawn in red and blue) with very similar frequencies. A beat pattern is characterized by a wave whose amplitude is changing at a regular rate. Observe that the beat pattern (drawn in green) repeatedly oscillates from zero amplitude to a large amplitude, back to zero amplitude throughout the pattern. Points of constructive interference (C.I.) and destructive interference (D.I.) are labeled on the diagram. When constructive interference occurs between two crests or two troughs, a loud sound is heard. This corresponds to a peak on the beat pattern (drawn in green). When destructive interference between a crest and a trough occurs, no sound is heard; this corresponds to a point of no displacement on the beat pattern. Since there is a clear relationship between the amplitude and the loudness, this beat pattern would be consistent with a wave that varies in volume at a regular rate.

Beat Frequency
The beat frequency refers to the rate at which the volume is heard to be oscillating from high to low volume. For example, if two complete cycles of high and low volumes are heard every second, the beat frequency is 2 Hz. The beat frequency is always equal to the difference in frequency of the two notes that interfere to produce the beats.
fbeat = |f1 - f2|
So if two sound waves with frequencies of 256 Hz and 254 Hz are played simultaneously, a beat frequency of 2 Hz will be detected.
Natural Frequency & Resonant Frequency
In sound applications, a resonant frequency is a natural frequency of vibration determined by the physical parameters of the vibrating object.
This same basic idea of physically determined natural frequencies applies throughout physics in mechanics, electricity and magnetism, and even throughout the realm of modern physics. Some of the implications of resonant frequencies are:
It is easy to get an object to vibrate at its resonant frequencies, hard to get it to vibrate at other frequencies. Swinging a child in a playground swing is an easy job because you are helped by its natural frequency. But can you swing it at some other frequency? With a tiny push on the swing each time it comes back to you, you can continue to build up the amplitude of swing. If you try to force it to swing a twice that frequency, you will find it very difficult, and might even lose teeth in the process!

A vibrating object will pick out its resonant frequencies from a complex excitation and vibrate at those frequencies, essentially "filtering out" other frequencies present in the excitation.
If you just whack a mass on a spring with a stick, the initial motion may be complex, but the main response will be to bob up and down at its natural frequency. The blow with the stick is a complex excitation with many frequency components, but the spring picks out its natural frequency and responds to that.
|
|
Most vibrating objects have multiple resonant frequencies.
Fundamental and Harmonics
The lowest resonant frequency of a vibrating object is called its fundamental frequency. Most vibrating objects have more than one resonant frequency and those used in musical instruments typically vibrate at harmonics of the fundamental. A harmonic is defined as an integer (whole number) multiple of the fundamental frequency.
- Vibrating strings, open cylindrical air columns, and conical air columns will vibrate at all harmonics of the fundamental.
- Cylinders with one end closed will vibrate with only odd harmonics of the fundamental.
- Vibrating membranes typically produce vibrations at harmonics, but also have some resonant frequencies which are not harmonics.
Open-End Air Columns
A cylindrical air column with both ends open will produce resonant standing waves at a fundamental frequency and at all harmonics.
- λn = 2L/n, for any integer n
- fn = nv/2L, for any integer n
Closed-End Air Columns
A cylindrical air column with one end closed will produce resonant standing waves at a fundamental frequency and at odd harmonics.
- λn = 4L/n, for any odd integer n
- fn = nv/4L, for any odd integer n
