Phase, In-Phase, Out-Of-Phase

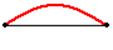
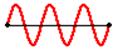
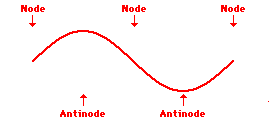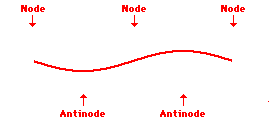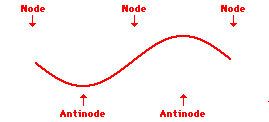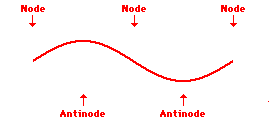
In order to be in phase, or out of phase, two waves must have the same frequency. When two waves are in phase, they oscillate together, their functions reach 0 value for same x values which repeat periodically AND their derivations have the same sing (+ or -).(Picture 1)

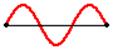
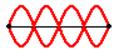
Out of phase waves are two waves whose functions reach 0 value for different x values. The amount of phase shift is denoted in degrees or radians. If two waves are completely out of phase (Picture 2), their phase shift is 180 degrees or pi radians. Their functions also reach 0 for same x values, but their derivations have opposite signs.

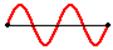
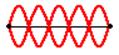
Waves in Picture 3 are out of phase by 90 degrees or pi/2 radians.

Principle of Superposition

The principle of superposition is stated as follows:

When two waves interfere, the resulting displacement of the medium at any location is the algebraic sum of the displacements of the individual waves at that same location.

The task of determining the complete shape of the entire medium during interference demands that the principle of superposition be applied for every point (or nearly every point) along the medium.

Constructive interference is a type of interference that occurs at any location along the medium where the two interfering waves have a displacement in the same direction.

Destructive interference is a type of interference that occurs at any location along the medium where the two interfering waves have a displacement in the opposite direction.

Standing Wave Pattern, Nodes, Anti-Nodes

In a standing wave pattern, there are points along the medium that appear to be standing still. standing wave patterns are produced in a medium when two waves of identical frequencies interfere in such a manner to produce points along the medium that always appear to be standing still. A standing wave pattern is not actually a wave; rather it is the pattern resulting from the presence of two waves of the same frequency with different directions of travel within the same medium. 

Standing waves are often demonstrated in a Physics class using a snakey that is vibrated by the teacher at one end and held fixed at the other end by a student. The waves reflect off the fixed end and interfere with the waves introduced by the teacher to produce this regular and repeating pattern known as a standing wave pattern.

Standing wave patterns can only be produced within the medium when it is vibrated at certain frequencies. Each frequency is associated with a different standing wave pattern. The lowest such frequency is called the fundamental frequency, and the integer multiples of the fundamental frequency are referred to as harmonics.

The points along the medium that appear to be standing still , sometimes described as points of no displacement, are referred to as nodes. There are other points along the medium that undergo vibrations between a large positive and large negative displacement. These are the points that undergo the maximum displacement during each vibrational cycle of the standing wave. These points are the opposite of nodes, and so they are called antinodes. The animation shown below depicts a rope vibrating with a standing wave pattern. The nodes and antinodes are labeled on the diagram. When a standing wave pattern is established in a medium, the nodes and the antinodes are always located at the same position along the medium; they are standing still. It is this characteristic that has earned the pattern the name standing wave (as opposed to traveling wave).

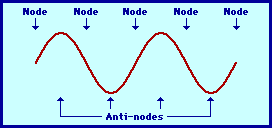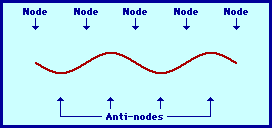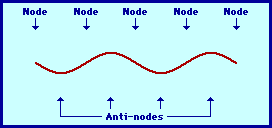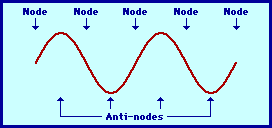
The simplest standing wave pattern that could be produced within a snakey is one that has points of no displacement (nodes) at the two ends of the snakey and one point of maximum displacement (antinode) in the middle. The animation below depicts the vibrational pattern observed when the medium is seen vibrating in this manner.

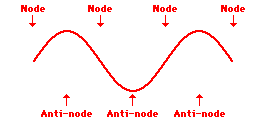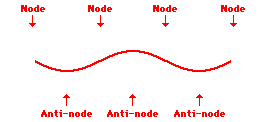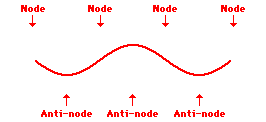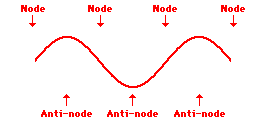
First Harmonic Standing Wave Pattern

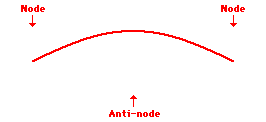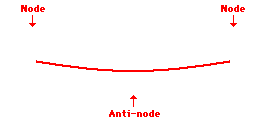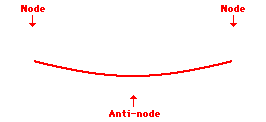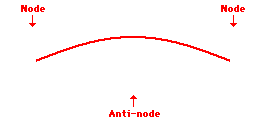
The above standing wave pattern is known as the first harmonic. It is the simplest wave pattern produced within the snakey and is obtained when the teacher introduced vibrations into the end of the medium at low frequencies.

Other wave patterns can be observed within the snakey when it is vibrated at greater frequencies. For instance, if the teacher vibrates the end with twice the frequency as that associated with the first harmonic, then a second standing wave pattern can be achieved. This standing wave pattern is characterized by nodes on the two ends of the snakey and an additional node in the exact center of the snakey. As in all standing wave patterns, every node is separated by an antinode. This pattern with three nodes and two antinodes is referred to as the second harmonic and is depicted in the animation shown below.

Second Harmonic Standing Wave Pattern

If the frequency at which the teacher vibrates the snakey is increased even more, then the third harmonic wave pattern can be produced within the snakey. The standing wave pattern for the third harmonic has an additional node and antinode between the ends of the snakey. The pattern is depicted in the animation shown below.

Third Harmonic Standing Wave Pattern

Observe that each consecutive harmonic is characterized by having one additional node and antinode compared to the previous one. The table below summarizes the features of the standing wave patterns for the first several harmonics.

Mathematical Relationships of String Length and Wavelength in Standing Wave Patterns