Temperature and its measurement
The relationship of temperature in Celsius and temperature in Kelvin can be expressed in the following equation:
T(Kelvin) = T(Celsius) + 273
Fahrenheit is a thermodynamic temperature scale, where the freezing point of water is 32 degrees Fahrenheit (℉) and the boiling point 212℉ (at standard atmospheric pressure). This puts the boiling and freezing points of water exactly 180 degrees apart. Therefore, a degree on the Fahrenheit scale is 1/180 of the interval between the freezing point and the boiling point of water. Absolute zero is defined as -459.67℉.
A temperature difference of 1℉ is the equivalent of a temperature difference 0.556℃.
Fahrenheit is a thermodynamic temperature scale, where the freezing point of water is 32 degrees Fahrenheit (℉) and the boiling point 212℉ (at standard atmospheric pressure). This puts the boiling and freezing points of water exactly 180 degrees apart. Therefore, a degree on the Fahrenheit scale is 1/180 of the interval between the freezing point and the boiling point of water. Absolute zero is defined as -459.67℉.
A temperature difference of 1℉ is the equivalent of a temperature difference 0.556℃.
Heat Transfer and Temperature Change
When a substance absorbs or loses heat, either its temperature will change or the phase of the substance will start to change, but NOT BOTH.
If the temperature changes, here is the equation to find out how much heat transfer is needed:
Given a substance of mass m, to change its temperature by ΔT, the amount of heat transfer needed Q is:
Q = mcΔT, where c is an instrinsic property of the substance called its "specific heat".
In above equation, the sign of ΔT and Q refer to whether temperature is going up or down, and heat is coming into the substnace or going out of the substance.
A calorie is defined as the amount of energy needed to raise the temperature of 1 gram of water by 1 degree of Celsius. 1 calorie ≈ 4.18 joules
If the phase of the substance changes, here is the quation to find out how much heat transfer is needed to complete the phase transformation:
Q = mL, where Q is heat transfer needed, m is mass of substance, and L is the "latent heat of transformation".
For a phase change between solid and liquid, L is called the latent heat of fusion.
For a phase change between liquid and gas, L is called the latent heat of vaporization.
Modes of Heat Transfer
Heat transfer can occur by
Conduction - Conduction is heat transfer by means of molecular agitation within a material without any motion of the material as a whole. For example, if one end of a metal rod is at a higher temperature, then energy will be transferred down the rod toward the colder end because the higher speed particles will collide with the slower ones with a net transfer of energy to the slower ones.
Convection - Convection is heat transfer by mass motion of a fluid such as air or water when the heated fluid is caused to move away from the source of heat, carrying energy with it. Convection above a hot surface occurs because hot air expands, becomes less dense, and rises. Hot water is likewise less dense than cold water and rises, causing convection currents which transport energy.
Radiation - Radiation through electromagnetic waves carrying energy.
Thermal Expansion
When the temperature of a substance changes, the substance changes its size.
For linear expansion, we have ΔL = αL0ΔT, where α is coefficient of linear expansion and L0 is initial length
For volume expansion, we have ΔV = ßV0ΔT, where ß is coefficient of volume expansion and V0 is initial volume
Note: for most solids, ß ≈ 3α, and for water between 0°C and 4°C, ß is negative.
Pressure and its measurement
Pressure is defined as force per unit area: P = F/A. The standard unit for pressure is the Pascal, which is a Newton per square meter: 1 Pa = 1 N/m2.
Atmospheric pressure, sometimes also called barometric pressure, is the pressure within the atmosphere of Earth. The standard atmosphere (symbol: atm) is a unit of pressure defined as 101.325 kPa.
PSI (pound-force per square inch) is another masurement unit for pressure: 1 psi = 6894.76 Pa.
Ideal Gas
As opposed to the real gases that you can find in the real world, ideal gas is an ideal state of gas that has the following 3 qualities:
- Molecules in the gas only have elastic collisions
- There are no inter-molecular forces and no gravity
- Molecules themselves are negligibly small compared to the volume of the gas.
Mole and Molar Mass
Mole is a measurement unit of the number of molecules in a gas. 1 mole = 6.02 x 1023 molecules
Molar mass, or "gram-molecular mass", is defined to be the mass (in unit of gram) of a substance that contains 1 mole of molecules.
For example, the molar mass of oxygen (O2) is 32 grams, which means 1 mole (6.02 x 1023) of oxygen has a mass of 32 grams.
The Ideal Gas Law
Standard form: PV = nRT, where P is pressure, V is volume, n is mole number, T is temperature, and R is universal gas constant at R=8.31 J / (mol * K)
Using Boltzmann constant: PV = NkT, where P is pressure, V is volumen, N is number of molecules, T is temperature, and k is Boltzmann constant at 1.38064852 × 10−23 joule per kelvin
Boyle's law (product of pressure and volume is constant): Put ideal gas in a sealed cylinder such that no gas can escape or enter. Place an external force on the piston at the top of the cylinder so that the pressure change causes the piston to move down. If F is the force applied, then work done W = F*h, since h = V/A (V for volume and A for cross-sectional area), we have W = FV/A = PV. In the process, if temperature of the gas in the chamber is kept constant, then P*V is a constant (PV=nRT).
Charles's law (ratio of volume to temperature is constant): holding pressure constant, the ratio of volume and temperature in an ideal gas will remain constant: V1/T1 = V2/T2.
Other forms:
P1V1 / T1 = P2V2 / T2
PV/T = constant
Kinetic-Molecular Theory
For an ideal gas, its total interal energy is the same as its thermal energy, which is purely in the form of molecular kinetic energy. Average kinetic energy per molecule = (3/2)kT, where k is Boltzmann constant, and T is temperature in Kelvin.
Using kinetic energy formula of (1/2) mv2, we have root-mean-square velocity Vrms = (3kT/m) squared
The First Law of Thermodynamics
Let ΔU be the change in internal molecular energy, Q is heat energy supplied to the system or taken out of the system, W be the work done to the system or by the system to its surroundings, then we have ΔU = Q + W. Note all 3 values can be positive or negative.
The first law of thermodynamics basically states the law of energy conservation.
Isothermal: constant temperature. Example: ice melting, water boiling. Another example (1st diagram below) is the experiment in Boyle's law: when piston is pushed down, work is done to the system. NOTE: in the experiment in Boyle's law, as the piston is pushed down (and hence work is done to the trapped gas), the gas's thermal energy goes up, but heat soon escapes through the cylinder wall, so its thermal energy goes back to its original level and that's how the temperature is kept constant.
Will ideal gas gain thermal energy as it is being compressed? The answer is yes.
The molecules speed up because they collide with the wall moving forward--- if you move a wall forward, a ball which bounces off the wall reflects going faster by twice the speed of the wall, because if you move along with the wall, it reflects at the same speed.
From 1st law of thermodynamics perspective, you are doing work to compress the gas, and the energy has to go somewhere.
From 2nd law of thermodynamics perspective, When you squeeze the gas, you are increasing your knowledge of where the molecules are, you are decreasing their wandering volume. This means that, if nothing else happens, you decrease their entropy. So something must happen to make you know less about the state of the gas molecules. If they are not allowed to dump heat and entropy into the exterior universe, the only thing that can happen is that they move faster, increasing your uncertainty about how fast they are going.
Isobaric: constant pressure. An example (2nd diagram below) of an isobaric system is a gas, being slowly heated or cooled, confined by a piston in a cylinder (and pushes it up as it expands). The work done by the system in an isobaric process is simply the pressure multiplied by the change in volume (W = P*V).
Isochoric: constant volume. An example (3rd diagram below) of this system is a gas in a box with fixed walls as it is being slowly heated or cooled. The work done is zero in an isochoric process.
Adiabatic: no gain or loss of heat to the system. An example of an adiabatic process is the vertical flow of air in the atmosphere; air expands and cools as it rises, and contracts and grows warmer as it descends.
Note in the 1st and 2nd and 4th diagrams below, the P and V changes are caused by work done on or by the system, not by heat change. Therefore the work done is equal to the area below the diagram (P*V). In the 3rd P/V diagram, the P change is caused by heat, so the work done is zero.
The Second Law of Thermodynamics
The entropy (randomness) of any isoloated system is always increasing. This implies that heat always flow spontanuously from hotter to cooler body and not vice versa.
The Third Law of Thermodynamics
The entropy (randomness) of a perfect crystal is zero when the temperature of the crystal is equal to absolute zero (0 K).
Efficiency of Heat Engine
Energy in the form of heat Qh comes into the heat engine from a high-temperature source. Some of the energy is converted into usefule work W, and the remainder is ejected as exhaust heat Qc into a low-temperature sink, and the system returns to its original state to run through the cycle again. Obviously:
W = Qh - Qc
And Efficiency of the heat engine e = (Qh - |Qc|)/Qh = 1 - |Qc|/Qh
Carnot Cycle
The most efficient heat engine follows the Carnot Cycle: https://chem.libretexts.org/Core/Physical_and_Theoretical_Chemistry/Thermodynamics/Thermodynamic_Cycles/Carnot_Cycle
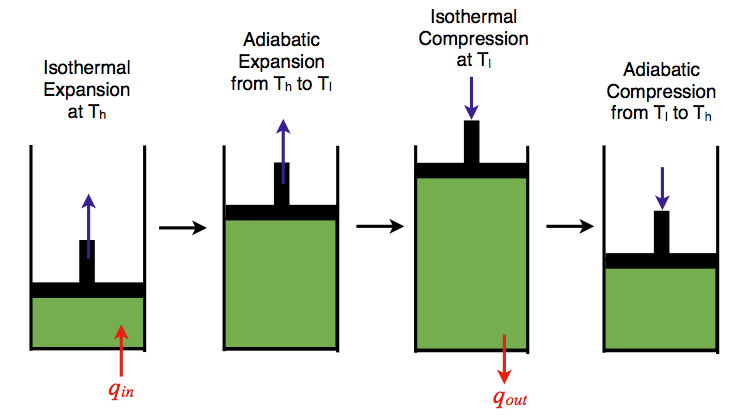
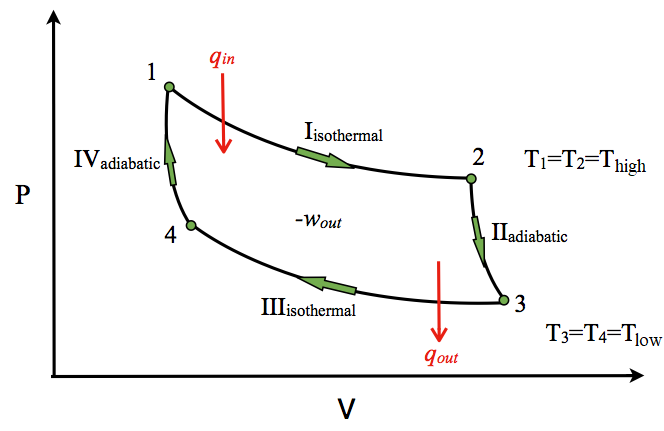
For the Carnot Cycle, efficiency can be re-written as:
e = (Th - Tc)/Th = 1 - Tc/Th
Triple Expansion Steam Engine
Review the following diagram and answer the question: why is the low-pressure cylinder larger than the intermediate-pressure cylinder and the intermediate-pressure cylinder larger than the high-pressure cylinder?